데이터 차원 축소를 위한 PCA(주성분 분석) 기법과 사용 예제

안녕하세요. 오늘은 데이터에 머신러닝 또는 Traditional 알고리즘을 사용하기에 앞서, 데이터의 주요 특징을 분석하는 방법인 PCA(Principal Component Analysis) 주성분 분석법에 대해 알아보겠습니다. PCA는 다차원 데이터의 주성분을 찾아주는 기법으로 복잡한 데이터의 차원을 축소시키기 위해 사용됩니다.

주로 수치 데이터에서 Support Vector Machine 이나 XGBoost 등의 머신러닝 분류 알고리즘으로 Classification을 수행하기 전, PCA로 데이터 차원을 축소시키면, 모델의 학습속도를 빠르게 할 수 있습니다. (다만, 차원을 축소시키는 과정에서, Classification에 필요한 정보들이 과하게 사라진 경우에는 모델이 학습 데이터에 Overfitting되는 문제가 발생할 수 있습니다.) 또한 PCA는 의료 영상 분야에서 시간 차를 두고 촬영된 이미지의 Registration에도 사용될 수 있습니다.

이번 포스팅에서는 PCA 주성분 분석법의 원리와 PCA가 의료영상 Registration에 어떻게 사용될 수 있는지에 대해 알아보도록 하겠습니다.

차원의 저주(Curse of Dimension)

데이터를 다루어야 하는 머신러닝 딥러닝 분야을 공부하신 분들이라면 차원의 저주라는 말은 한번쯤 들어보셨을 겁니다. 차원의 저주란 데이터의 차원이 증가할수록, 학습에 필요한 데이터의 수가 기하급수적으로 증가하기에, 학습 데이터가 부족하여 데이터 학습 성능이 떨어지는 현상을 말합니다. 따라서 이러한 경우, 데이터의 차원을 줄이거나 데이터 수를 늘려야 합니다. 여기서 데이터의 차원이 하나 증가한다는 것은 데이터의 변수(또는 feature)가 하나 증가하는 것을 의미합니다.

이렇게만 설명하면, 차원의 저주가 완벽히 이해되지 않을 수 있기에 간단한 예를 들어 보겠습니다. 공장 장비에서 수집된 수치데이터를 통해 제조품의 불량/정상에 대한 Classification을 수행한다고 하였을 때, 데이터가 x 변수 하나로 이루어진 경우와 (x,y,z) 세가지 변수로 이루어진 경우를 생각해봅시다. 먼저 데이터가 x변수 하나로 이루어진 경우에는 불량/정상 분류를 위해서는 x 에 대한 분류선 하나가 필요하므로, 분류선을 기준으로 서로 반대편에 있는 2개의 데이터가 필요합니다. 반면에 데이터가 (x,y,z) 3개의 변수로 구성된 경우에는 불량/정상 분류를 위해서 x,y,z축 각각에 대한 분류선이 필요하므로, 최소 8개의 데이터가 필요합니다. (아래 그림 1 참고)

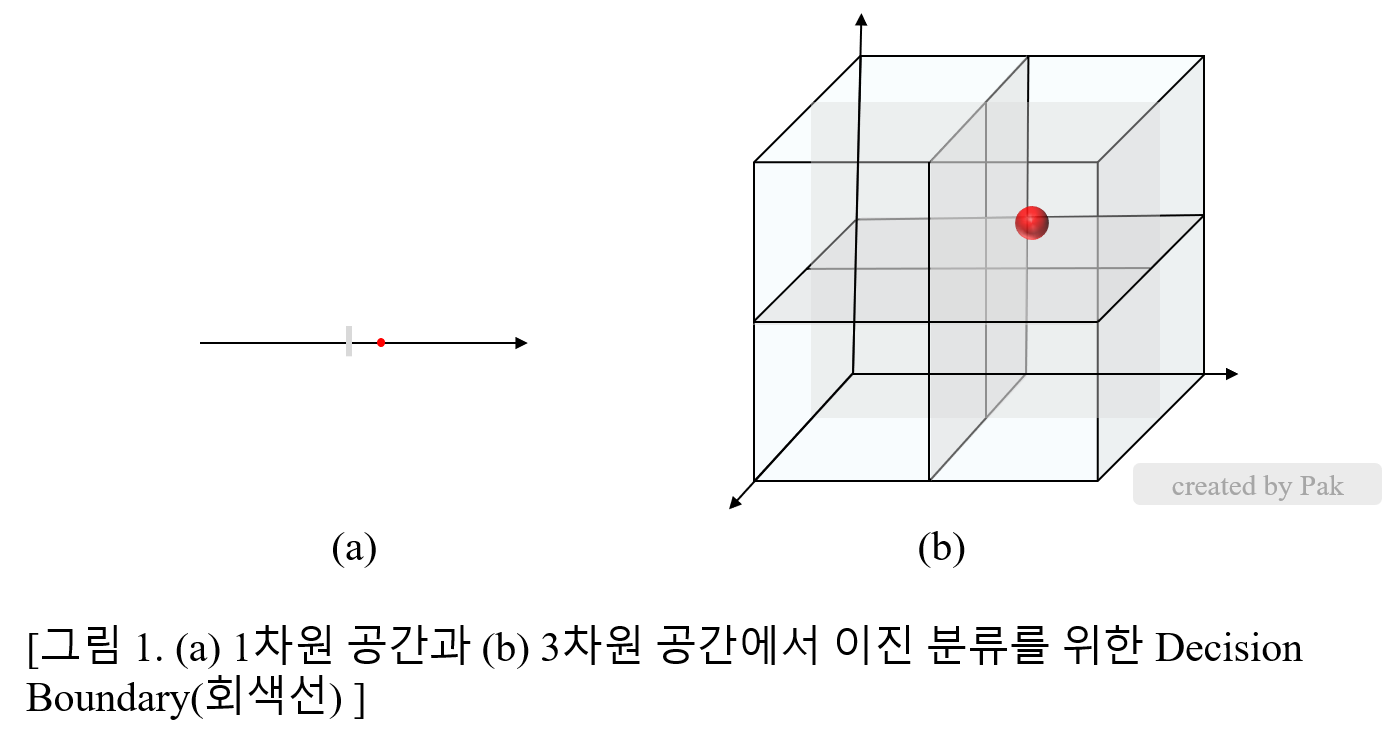
따라서 데이터가 부족한 경우 데이터의 차원을 축소시키는 것이 학습에 도움이 될 수 있습니다. 데이터의 차원을 축소시키는 방법 중 하나인 PCA에 대해 알아보겠습니다.

PCA 주성분 분석

PCA는 데이터의 분산을 최대화시키는 투영축을 찾는 과정입니다. 이 투영 축이 데이터의 주축을 의미합니다. 그렇다면, 이 주축을 어떻게 찾을까요? n개의 변수를 가진 k개의 데이터가 있다고 합시다. 이 데이터 셋의 변수값 별로 평균을 0으로 만든 데이터셋을 $\vec{X}$라고 지칭합시다. 이 데이터 셋 $\vec{X}$를 단위벡터 $\vec{e}$인 임의의 축으로 projection 하는 것은 $\vec{X}\cdot\vec{e}$로 표현할 수 있습니다. 이 $\vec{X}\vec{e}$의 분산 $Var$[$\vec{X}\cdot\vec{e}$]를 최대화시키는 임의의 축 $\vec{e}$를 찾으면 됩니다.

\begin{align} maximize \space Var[\vec{X}\cdot\vec{e}] \end{align} \begin{align} = maximize \space {\vec{e}^{T} C\vec{e}} \space (C=\frac{X^{T}X}{k-1}) \end{align}

이를 라그랑제 승수법을 이용해 풀면 다음과 같습니다.

\begin{align} C\vec{e}=\lambda\vec{e} \end{align}

여기서 $\vec{e}$는 공분산 $C$ 의 고유벡터, $\lambda$ 는 $C$의 고유값을 의미합니다. 이 고유벡터 $\vec{e}$의 열 벡터들이 $X$의 주축을 나타냅니다.
$X$의 차원 수만큼의 고유값이 구해지는데, 고유값 $\lambda_1$을 $(C - \lambda)\vec{e} = 0$ 에 대입했을 때, 계산되는 $\vec{e}$ 값이 고유값 $\lambda_1$에 해당하는 고유벡터입니다. 가장 큰 고유값에 해당하는 고유벡터가 $X$의 가장 중요한 주축을 의미합니다. 고유벡터와 고유값의 의미에 대한 이해가 필요하신 분은 위 사이트를 참고하시면 됩니다. 단계적으로 친절하게 설명해놓으셨습니다.

제가 PCA의 원리를 공부하면서, 궁금했던 것이 있는데, 아직 이에 대한 답을 생각해내지 못하였습니다. PCA를 수행하기 전, 데이터 변수 값 별로 평균을 0으로 만드는 zero-centering 을 하는데, 이것을 왜 수행하는 것인지…? 뉴럴넷 학습전 데이터를 zero mean, one varaiance로 data normalization을 해주는 이유와 비슷한 이유일까요..? 아시는 분 답변 부탁드립니다..

참고

뉴럴넷 gradient 기반의 학습에서 data normalization을 해주는 이유는 두가지로 생각해볼 수 있습니다. 첫번째 이유는 데이터가 정규화되어있지 않은 상태에서 Gradient descent 기반의 학습을 하게 되면 데이터 변수 별로 range가 다른 상태인데, weight update시 사용하는 learning rate는 모든 weight에 대해 동일한 값을 사용하므로 \vec{W}의 각 요소 들이 update되는 크기가 천차만별이 되어서 gradient descent로 최적 값 찾아가는 과정에서 overshooting이 발생할 수 있습니다. 그러면 weight가 최적값으로 최단 경로로 이동하지 못하고 지그재그로 이동을 하게 되므로 학습이 비효율적으로 진행됩니다.

두번째 이유는 앞의 내용에 포함되는 내용인데, 데이터 zero-centering을 안해주면, 입력값이 positive인 경우 $\vec{W}=(w_1,w_2)$ 업데이트 시, $w_1$이 양의 방향, $w_2$가 음의 방향으로 업데이트 되어야 하는 경우, $w_1$과 $w_2$가 모두 positive 또는 negative 방향으로 밖에 업데이트가 안되기 때문에 한번 업데이트로는 원하는 방향으로 이동을 못하고 여러번 업데이트를 통해 이동을 해야하는 문제가 발생하기 때문에 zero-centering을 수행합니다.

PCA 기법 사용 예제 - C/C++ pcl 라이브러리를 사용한 STL Registation

STL포맷에 담긴, 두개의 동일한 3차원 치아 데이터를 Registration을 할 때 데이터의 주축을 찾아서 초기 정합을 하기 위해 PCA 주성분 분석을 사용할 수 있습니다. Registration의 기준이 되는 데이터를 reference 데이터, 움직일 데이터를 floating 데이터라고 부르겠습니다. 두 데이터의 Restration은 다음과 같은 순서로 진행됩니다.

1. 먼저 Normal vector와 Triangle points facet으로 구성된 STL데이터에서 point cloud를 추출합니다.
2. reference와 floating point cloud에 대한 각 centroid값을 구하여 floating의 center값을 reference의 center위치로 맞춰줍니다.  
3. reference와 floating 데이터의 주성분 분석을 통해 각각 3개의 주축을 찾습니다. 
4. floating의 주축의 방향과 reference 주축의 방향사이의 변환 T을 구합니다. 
5. floating point cloud에 변환 T를 곱하여 이동시킵니다. 
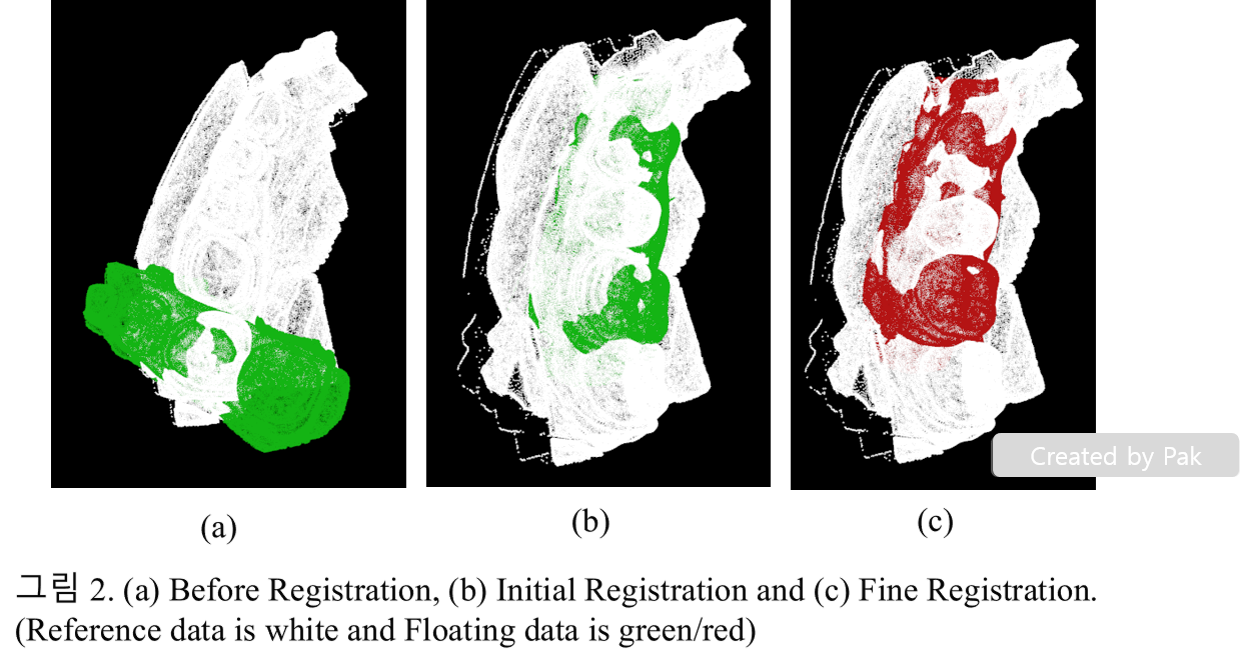
이렇게 하면 reference와 floating데이터의 point cloud주축을 일치시키는 initial registration이 끝났습니다.
그 다음에는 Iterative Closest Point(ICP)알고리즘을 사용하여, point cloud의 point 각각의 위치를 일치시키는 fine registration을 수행합니다. 

Regisration 코드는 위 사이트에 올려놓았습니다. 그림 2에서 정합 전 모습과 초기 정합, 정밀 정합 결과를 확인할 수 있습니다.

결론

오늘은 PCA의 원리와 사용예제에 대해 알아보았습니다.e PCA는 데이터의 분산을 최대화하는 주축을 찾아주는 알고리즘으로 데이터의 차원을 축소시키는데 사용될 수 있음을 배웠습니다. 따라서 PCA는 SVM과 같은 머신러닝 분류기를 사용하기에 앞서 데이터 전처리방법으로 사용될 수 있습니다. 또한 PCA는 데이터의 주축을 찾아주기에, 두 Point cloud를 일치시키는 작업에서 초기 Registration방법으로 사용될 수도 있었습니다.

오늘 제 포스팅을 읽으시고 이해가 안되시는 사항이 있다면 댓글로 질문주세요~